本ブログの御訪問ありがとうございます
機械設計歴20年以上のtsurfと言います
今回は以下に関する記事です
【機械設計の物理】
慣性モーメント(イナーシャ)の式
の一例と解説
⇩本記事は以下の方にオススメです⇩

未経験機械設計者
よく使う慣性モーメントの式と使い方をを教えてよ
⇩本記事を読むと以下が わかります⇩

よく使う慣性モーメントの式を
以下まとめました
目次
①慣性モーメントの式について
慣性モーメントとは
断面における『回転軸に対して各微小質点の加速させにくさ』の積分です。
ですので
外側にある質点ほど、加速させにくくなります。
外径が大きくなればなるほど
乗数的に大きくなっていくのが、式を見れば わかると思います
②回転する直方体

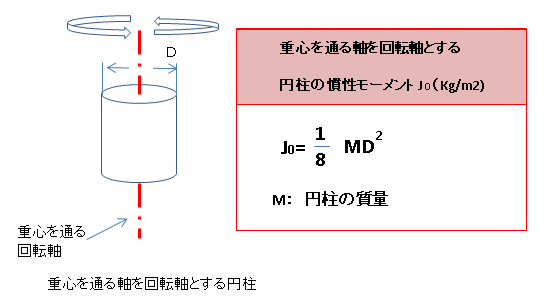
③回転する円柱
慣性モーメントの式
直動駆動機構での慣性モーメント計算例
| 機構 | 応用例 | 備考 |
|---|---|---|
| ボールネジ 機構 |
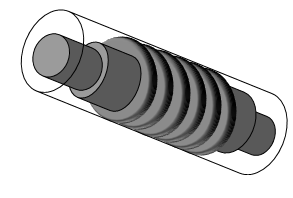
ボールネジ | ボールネジ外径を最外径とした 円柱として近似計算する
|
④回転する中空円柱
慣性モーメントの式

直動駆動機構での慣性モーメント計算例
| 機構 | 応用例 | 備考 |
|---|---|---|
| ボールネジ機構
|
ベアリング内輪 |
--- |
| ベアリングナット | --- | |
| カップリング | --- | |
| 止め輪 |
小さいので 無視 |
|
|
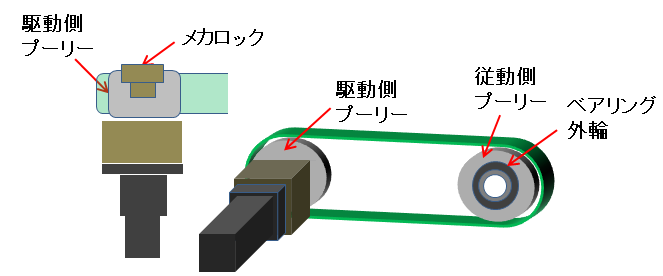
ベルト駆動機構
|
||
| 駆動側プーリー | --- | |
| 従動側プーリー | --- | |
| メカロック | --- |
注意点
中実円柱と中空円柱の式を比べると
一瞬 中空円柱のほうが 慣性モーメントが大きくなるイメージがあります
しかし 中空円柱のほうが 質量が小さいので
実際の慣性モーメントの計算値は 当然 中空円柱のほうが小さくなります
⑤円運動する物体の慣性モーメント
回転中心が重心ではない場合の慣性モーメントです
この式は重要です

⑥複合形状の慣性モーメント
応用として 以下の図のような場合を解説します
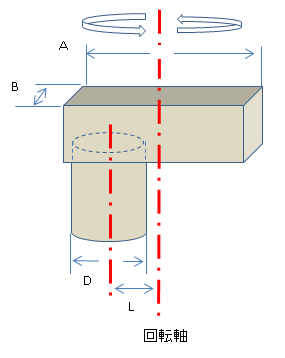
以下のように バラバラにして個別に計算し足します
J1:重心を通る軸を回転軸とする直方体の慣性モーメント
+
J2:重心以外の軸を回転軸とする円柱の慣性モーメント

⑦まとめ
上記で求めた慣性モーメントに角加速度をかければ
加速トルクが算出できます。
以下の記事を御参照ください。
本記事は以上です。
最後までお読みいただきありがとうございます。