本ブログの御訪問ありがとうございます。
機械設計歴20年以上のtsurfと言います。
今回は以下に関する記事です。
エアシリンダの選定計算(推力計算)
基礎と 計算例
⇩本記事は機械設計初心社の方で以下の方にオススメです⇩

未経験機械設計者
エアシリンダーの
選定計算について
知りたいんだけど
⇩本記事を読むと以下が わかります⇩

エアシリンダー
の選定計算 基礎と
計算の実例を
解説します
①前提知識
基礎
エアシリンダーに関わらず、駆動系を使いワークを搬送させる場合、
駆動系の選定に共通して必要なのは、以下の式です。
必要推力(N)=外部負荷力(N)+加速力(N)
このあたり 詳しく知りたい方は 以下の記事の御参照をお願いします
- 外部負荷力(詳しくは後述します)
垂直搬送であれば重力
水平搬送であれば摩擦力 - 加速力(詳しくは後述します)
物体を動かし始める時の力です
加速を与えることによって 最終的に等速直線運動ができます
力は加速度と質量に比例します
推力計算の目的
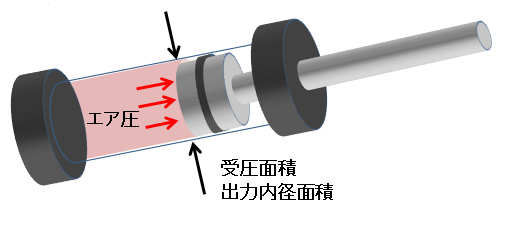
エアシリンダーの選定において 重要なのは 出力径の計算です。
出力径の面積 × エア圧で そのエアシリンダーの出せる推力が、
決まってくるからです。
②結論:推力計算方法
計算解説用モデル
以下のモデルで、推力計算の解説を行います。

まずは、外部負荷力を求める
上述したモデルの直動する部品は、以下となります。
- ワーク
- ワーク受け
- ベースプレート
- フローティングジョイント
- LMスライドブロック(カタログに記載あり)
上記の直動する部品の質量の合計を以下とします。
直動部品合計質量 M(Kg)
垂直搬送の場合の外部負荷力(重力 )をFmv
水平搬送の場合の外部負荷力(摩擦力)をFmh
とすると各外部負荷力は以下の式になります。
垂直搬送による重力 Fm v = Mg
水平搬送による摩擦力 Fm h = µMg
M:直動部品合計質量 (Kg)
g:重力加速度 9.8 (m/sec²)
µ:摩擦係数 0.1(無次元) *1
加速力を求める
加速力は 質量 × 加速度として以下で求められます
加速度についての基礎的な計算例は以下となります。
| ● | 等速直線運動速度: | 0.2 | (m/sec) |
| ● | 加速時間: | 0.5 | (sec) |
上記の場合 以下となります
0.2(m/sec) ÷ 0.5(sec)
=0.4(m/sec²)
-注意-
加速度に関しては、モーターのように制御できないので参考値です。
では実際のエアシリンダーの運転条件から
加速時間をどうやって求めればいいのでしょうか?
私が以前 空圧メーカーの講習を受けた際に
経験則的に求められる加減速時間と等速直線走行時間は
以下になるとのことです。
全運転時間をt(sec)とすると
- 加速時間 :0.1t(sec)
- 等速直線走行時間:0.8t(sec)
- 原則時間 :0.1t(sec)
となりますが、この計算で算出される速度が
実現可能速度かどうかは、各メーカーのカタログで
確認してください。
⑤実際の計算例で詳しく解説します。
外部負荷力と加速力から出力径の算出
上記で 必要推力はFm+Faということになります。
従って、
エアシリンダの推力が 必要推力を上回ればといわけです。
エアシリンダ自体の推力は
- 出力外径D(mm)
- エア圧をP(MPa=N/mm²)
とすると、以下の計算式となります
(D/2)² × π × P>Fa + Fm
よって エアシリンダーの出力径D(mm)は
安全率等を追加して 以下となります。
D= 2 × √{ Y ×(Fa+Fm) /(P × π)}
Fa : 加速力 (N)
Fm: 外部負荷力 (N)
P : エア圧 (N/mm²<=MPa>)*3
π : 円周力3.14(無次元)
Y : 安全率 (無次元)*4
しかし 上述で求めたシリンダーの出力径は
まだ仮決定状態です。
いくつかの確認事項が必要です。
③確認1 ロッド引き込み時条件の確認
概要
エアシリンダの出力内径が決定しました。
しかし 引き込み側は 出力が減少するので確認の計算をします。
何故なら、 ロッド付きエアシリンダーの場合
押し出し動作と引き込み動作では以下の理由から
出力が違ってきますので以下の2ケースの確認計算が必要となります。
押し出し動作は計算を終了して、仮決定の状態ですので、
引き込み動作の検証をします
| ロッド 押し出し 方向 |
|
|---|---|
| ロッド 引き込み 方向 |
 |
解説モデルの例では 以下のように 引き込み方向では
ワークのが無いという違いがあります

つまり
外部負荷力と摩擦力の計算式で直動部質量を求めていますが
解説モデルの例においては
直動部質量をワークの重さを引いたものとして計算します
確認内容計算
以下であることを確認します
ロッド引き込み側出力F”(N)
> ワーク無での必要推力Fm”+Fa”(N)
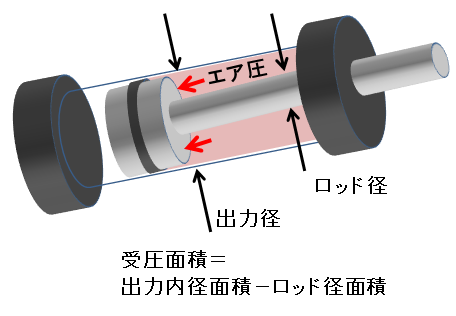
F”=P × {π × (D²-d²)/ 4}
P : エア圧 (N/mm²)
π : 円周力3.14(無次元)
D : 出力内径 (mm)
d : ロッド径 (mm) *5
Fm” + Fa"
Fm” : ワーク無しでの外部負荷力 (N)
Fa” : ワーク無しでの加速力 (N)
注意点
以下のケースの場合
引き込み時は、重力で落ちる方向にあります
加速度が9.8m/sec以内であれば確認の必要ありません。

④確認2 許容運動エネルギー確認
エアシリンダーは構造上ボディは、
安価性、制作のスピード性のためにアルミの押出成形などで
作られており、剛性は高くありません。
そこで許容エネルギーの確認をします。
以下の記事を御参照お願いします
⑤実際の計算例
モデル解説
以下のモデルを想定します。
以下の機構を用いて、ワークを300mm水平搬送させます。

走行条件
| 運転姿勢 | : | 水平 | |
| ストローク | : | 300 | (mm) |
| 移動時間 | : | 3 | (sec) |
| エア圧 | : | 0.5 | (MPa) |
上記の機構において
構想段階において、想定できる部品は以下となります。
初期想定可能部品M(kg)
| ワーク | : | 1 | (Kg) |
| ワーク受け | : | 1 | (Kg) |
| ベースプレート | : | 5 | (Kg) |
仮選定部品
| LMガイドスライドブロック | : | 0.05 | (Kg) | 個数1ヶ |
| フローティングジョイント(仮推定) | : | 0.05 | (Kg) | 個数1ヶ |
LMガイドについては、
設計段階で変更となるかもしれませんが、
総重量からある程度選定が可能です。
フローティングジョイントついては、
エアシリンダーの型式がわからなくては、選定の仕様がありませんが、
とりあえず50g程度としておき、想定と違っていたら、正規の重量で
計算しなおします。
以上より以下となります。
仮設定部品総重量:7.2(Kg)
エアシリンダーの選定においての第一目的は、あくまで
エアシリンダー内径の算出です。
手順1
運転パターンから加速度の算出
運転パターンを検討します。
目的は加速時間と運転速度V”を求めて加速力を算出したからです。
まず エアシリンダは制御的に加速時間などが制御できません。
従って等速直線運動時間は、経験則的に全走行時間の0.8倍
となるのだそうです。
以下のような運転パターンができました。

では 運転速度v”をもとめましょう。
グラフを以下のように、考えます。

台形から長方形になりましたので、簡単にv”を求める
ことが可能となりました。
運転速度v”=
{2.4(sec)+0.3(sec)} × V(m/sec) =0.3(m)より
=0.11(m/sec)
上記で求めた速度はカタログで
確認してください。
ではここから加速度を求めましょう。
加速度a(m/sec²)
=運転速度v”0.11(m/sec) ÷ 加速時間0.3(sec)
=0.37(m/sec²)
手順2
外部摩擦力と加速力の算出
⇩外部摩擦力を求めます。⇩
外部摩擦力Fm(N)
=仮設定部品総重量M 7.2(kg) × 重力加速度9.8(m/sec²)
× 摩擦係数0.1(無次元)
=7.05(N)
⇩加速力を求めます。⇩
加速力Fa(N)
=仮設定部品総重量M 7.2(kg) × 加速度0.37(m/sec²)
=2.7(N)
-注意-
摩擦係数は垂直搬送の場合1で計算します。
手順3
外部摩擦力と加速力の算出
シリンダー出力内径の式は以下となります。
D= 2 × √{ Y ×(Fa+Fm) /(P × π)}
以下より
| 加速力 | Fa | : | 2.7 | (N) |
| 外部摩擦力 | Fm | : | 7.05 | (N) |
| エア圧 | P | : | 0.5 | (N/mm²(=MPa)) |
| 安全率 | Y | : | 1.5 | (無次元) |
仮決定エアシリンダー出力内径D(mm)
=Φ6.10(mm) 既製品に照らし合わせるとΦ10mmが妥当でしょう
≒ Φ10(mm)
ここで 出力内径Φ10とのことですので、
フローティングジョインをΦ10用のものを確認します。
すると10gでした。
選定計算としては50gでの計算ですので、多少の誤差と見なします。
手順4
引き込み駆動力の確認
引き込み時は ワークを受け渡すためワークはありません。
従って搬送重量は以下となります。
⇩引込側仮設定部品総重量を求めます。⇩
引込時仮設定部品総重量M”
=仮設定部品総重量7.2(kg) - ワーク重量1(kg)
=6.2(kg)
⇩引込側外部摩擦力を求めます。⇩
引込側外部摩擦力Fm”(N)
=引込時仮設定部品総重量M” 6.2(kg) × 重力加速度9.8(m/sec²)
× 摩擦係数0.1(無次元)
=6.07(N)
⇩引込側加速力を求めます。⇩
引込側加速力Fa"(N)
=仮設定部品総重量M 6.2(kg) × 加速度0.37(m/sec²)
=2.3(N)
-注意-
摩擦係数は垂直搬送の場合1で計算します。
上記より
引込側必要推力F"(N)
=引込側外部摩擦力Fm” 6.07(N) + 引込側加速力Fa" 2.3(N)
=8.37(N)
今回選定しているΦ10のエアシリンダーのロッド径はΦ4です
従って引き込み側の出力の計算式は以下です
Fs”=P × {π × (D²-d²)/4}
以下より
| 出力内径 | D | : | 10 | (mm) |
| ロッド径 | d | : | 4 | (mm) |
| エア圧 | P | : | 0.5 | (N/mm²(=MPa)) |
仮決定エアシリンダー引込側出力Fs”(N)
≒ 33(N)
従って
仮決定エアシリンダー引込側出力Fs"(N) 33(N)
>引込側必要出力F”(N) 8.37(N)
なので仮決定エアシリンダーはΦ10で問題なし
手順5 許容運動エネルギーの確認
では今回の運動エネルギーを求めます。
運動エネルギーの公式は以下となります。

| 重量 | : | M | (kg) |
| 速度 | : | V | (m/sec) |
今回の運動エネルギーK(J)
=(1/2) × 質量M 7.2(Kg) × {運転速度V" 0.11(m/sec²)}²
=0.04(J)
ここで Φ10のエアシリンダーラバークッションでは
許容運動エネルギー0.035(J)をオーバーしてしまっています。
ここで選択肢は2つあります。
- 選択肢1 エアークッションのものに変更
- 選択肢2 出力内径を1ランク上のものにする
ここで私の選択は 以下です
選択肢2 出力内径を1ランク上のものにする
理由は
エアクッション付きだと端面で速度が遅くなる可能性が
あるからです。
Φ10のエアシリンダの1ランク上は、Φ16のエアシリンダです。
ここで Φ16のエアシリンダーラバークッションは
許容運動エネルギー0.09(J)で安全率も2倍以上です。
従って、
今回の機構で使用するエアシリンダの
出力内径はΦ16とする。
<注>このように、水平搬送の外部負荷力である摩擦力は
垂直搬送の重力より はるかに小さいため、
必要推力が小さくて済む場合が多いです。
従って、推力だけ見て、小さなエアシリンダを選定してしまうと
許容運動エネルギーでNGの場合が多いです。
⑥まとめ
- エアシリンダーの選定計算は、それほど複雑ではありません。
- 出力=出力径面積 × エア圧というシンプルなものです。
- ロッド付きエアシリンダーは、引込動作時、出力が
ロッドの径分、落ちることに、留意する必要があります。 - 許容運動エネルギーの確認も必須です。
特に推力が小さくて済む、水平搬送でNGとなる場合が多いです。
本記事は以上です
最後までお読み頂きありがとうございます
