本ブログの御訪問ありがとうございます。
機械設計歴20年以上のtsurfと言います。
今回は以下に関する記事です。
【機械設計の物理】力の分解
(斜面上の物体に掛かる力と動かすための力)
⇩本記事は機械設計初心者の方で以下の方にオススメです⇩

未経験機械設計者
機械設計に使える
基礎的な物理を
教えて欲しい
⇩本記事を読むと以下が わかります⇩

今回は力の分解その2として
斜面上にある物体に
掛かる力と動かすための力
を解説します
①力の分解解説モデル
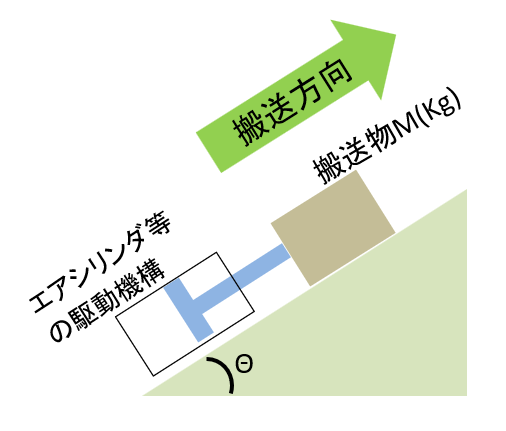
今 以下の図のように、
角度Θ°の斜面上に搬送物があります。
ここで、この駆動機構が搬送物を斜面沿いに
搬送するために必要な力を解説します。
②結論
駆動機構が必要とする外部負荷力Fk(N)は、
以下となります。
Fk=Ma+(Mg・sinΘ+μMg・cosΘ)
| Θ | ⇒ | 斜面の角度 | (°)もしくは (radian) |
|---|---|---|---|
| M | ⇒ | 搬送物の質量 | (Kg) |
| a | ⇒ | 搬送させる際の加速度 | (m/sec²) |
| g | ⇒ | 重力加速度(9.8) | (m/sec²) |
| μ | ⇒ | 摩擦係数 | (無次元) |
このMaの部分に関しては加速力となりますので
以下の記事を参照してください。
今回は、外部負荷力をメインとして
Mg・sinΘ+μMg・cosΘの部分
を外部負荷力Ft(N)として解説します。
③搬送物に必要な力(外部負荷力)
概要
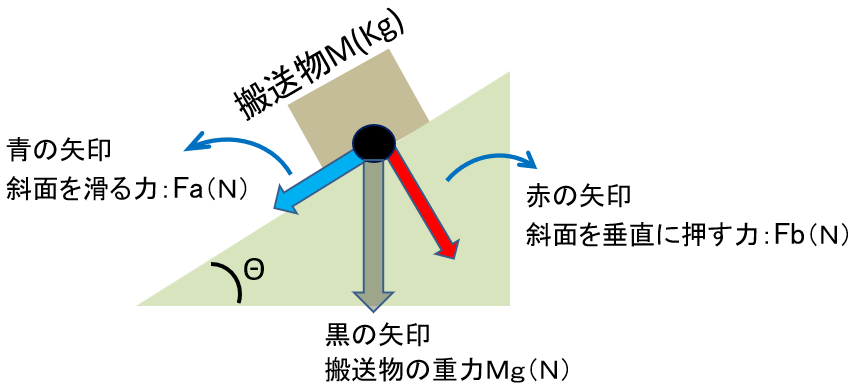
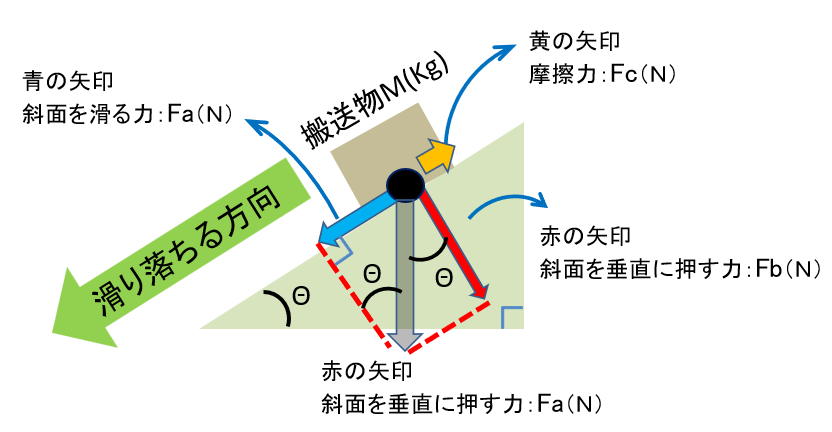
斜面によって物体に掛かる力は以下に分解されます。
ここで駆動機構に必要な力は、加速力を除けば
滑り落ちる力に対抗する力Faが必要になりますね。
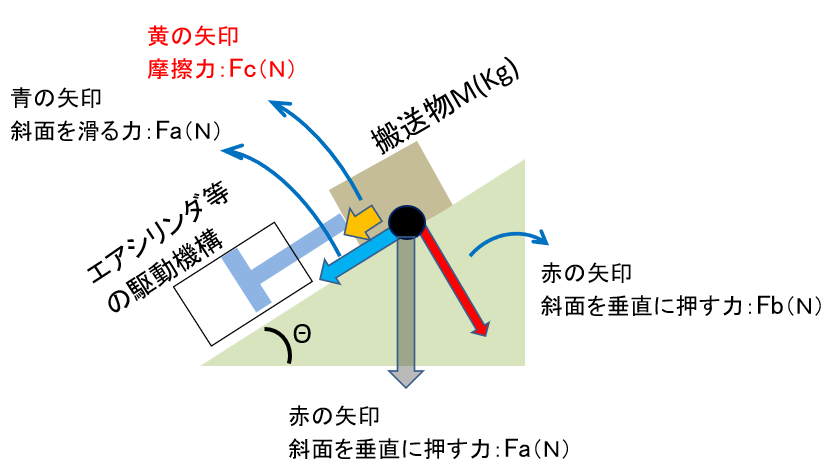
しかし それだけではありません。
駆動機構が斜面に沿って搬送しようとするときに
斜面と搬送物に摩擦力が生じます。
なので以下の赤字が追加されます。
ここで 分解された力に補助線を追加していきましょう。
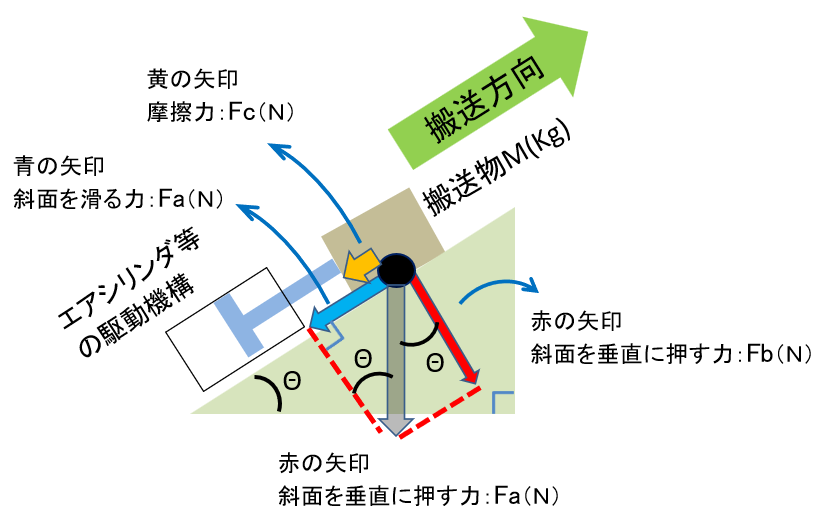
最終的に搬送に必要な外部負荷力
ここでまとめると搬送に必要な外部負荷力は、
- 斜面を滑り落ちる力Fa(N)
- 斜面と搬送物の摩擦力Fc(N)
となります。
④搬送に必要な外部負荷力Ft(N)の算出
斜面を滑り落ちる力Fa(N)
以下の図より、

青い矢印:斜面を滑る落ちる力Fa(N)は
以下となります。
Fa=Mg・sinθ
| Θ | ⇒ | 斜面の角度 | (°)もしくは (radian) |
|---|---|---|---|
| M | ⇒ | 搬送物の質量 | (Kg) |
| g | ⇒ | 重力加速度(9.8) | (m/sec²) |
搬送物と斜面の摩擦力Fc(N)
摩擦力とは、接地面に垂直に掛かる力に比例して
進行方向に対して妨害する力です。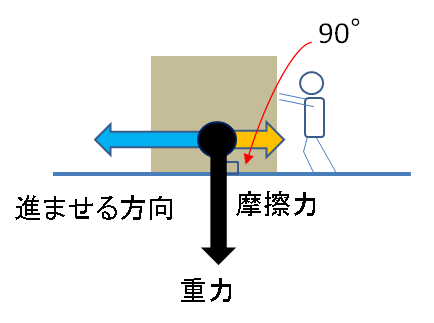
摩擦力は以下の式で算出します。
摩擦力(N)
=摩擦係数(無次元) × 接地面に垂直に掛かる力(N)
となります。
上図の場合、接地面に垂直に掛かる力は重力なので
摩擦力(N)
=摩擦係数(無次元) × 重力(N)
となります。
なので、今回は以下の図より
接地面(今回は斜面)に垂直に掛かる力は、
赤矢印のFb(N)となります。
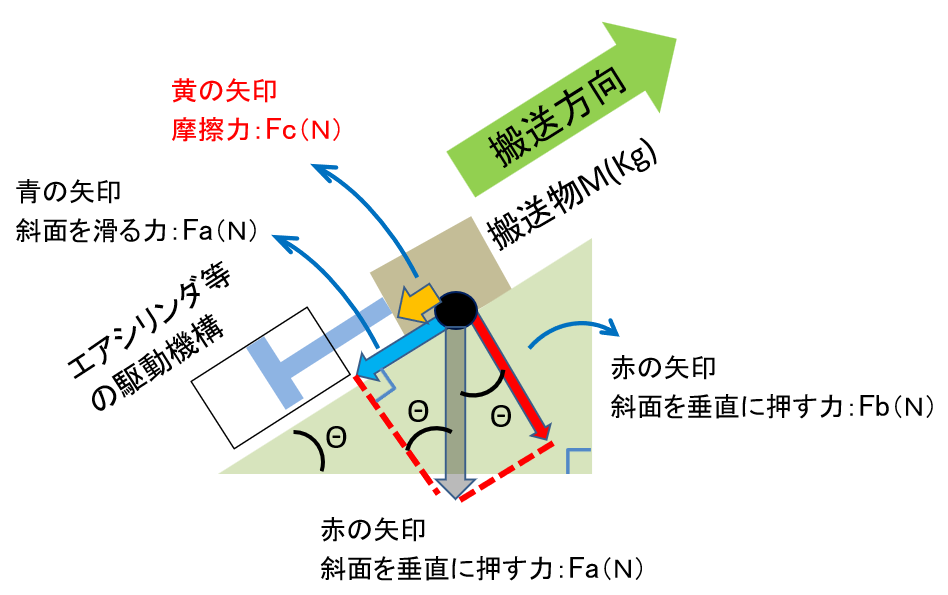
Fb=Mg・cosΘなので
黄色い矢印:摩擦力Fc(N)は以下となります。
Fc=µMg・cosθ
| Θ | ⇒ | 斜面の角度 | (°)もしくは (radian) |
|---|---|---|---|
| M | ⇒ | 搬送物の質量 | (Kg) |
| g | ⇒ | 重力加速度(9.8) | (m/sec²) |
| μ | ⇒ | 摩擦係数 | (無次元) |
斜面上の搬送物を動かすために
必要な外部負荷力
つまり、以下の図において

駆動機構が必要な外部負負荷力Ft(N)は、
以下となります。
Ft=Mg・sinΘ+μMg・cosΘ
| Θ | ⇒ | 斜面の角度 | (°)もしくは (radian) |
|---|---|---|---|
| M | ⇒ | 搬送物の質量 | (Kg) |
| g | ⇒ | 重力加速度(9.8) | (m/sec²) |
| μ | ⇒ | 摩擦係数 | (無次元) |
⑤駆動機構が搬送物を斜面に押し上げる力の式の応用
概要
今回の式で御紹介した
斜面の外部負荷力Ft(N)の式ですが
駆動系を考えた場合には当然今回触れなかった加速力も
必要になります。
すると、駆動系が必要な力Fk(N)は以下の式となります。
Fk=Ma+(Mg・sinΘ+μMg・cosΘ)
| Θ | ⇒ | 斜面の角度 | (°)もしくは (radian) |
|---|---|---|---|
| M | ⇒ | 搬送物の質量 | (Kg) |
| a | ⇒ | 搬送させる際の加速度 | (m/sec²) |
| g | ⇒ | 重力加速度(9.8) | (m/sec²) |
| μ | ⇒ | 摩擦係数 | (無次元) |
実は この式は、どのようなケースにも応用できる
汎用性のある式なのです。
水平時に必要な駆動力Fkh(N)
このΘに水平時である0°を代入します。
Fkh=Ma+Mg・sin(0°)+μMg・cos(0°)
sin(0°)=0 cos(0°)=1 より
水平時の駆動系の搬送力Fkh (N)
は以下となります。
Fkh=Ma+μMg
| M | ⇒ | 搬送物の質量 | (Kg) |
|---|---|---|---|
| a | ⇒ | 搬送させる際の加速度 | (m/sec²) |
| g | ⇒ | 重力加速度(9.8) | (m/sec²) |
| μ | ⇒ | 摩擦係数 | (無次元) |
垂直時に必要な駆動力Fkv(N)
このΘに垂直時である90°を代入します。
Fkv=Ma+Mg・sin(90°)+μMg・cos(90°)
sin(90°)=1 cos(90°)=0 より
垂直時の駆動系の搬送力Fkv(N)
は以下となります。
Fkv=Ma+Mg
| M | ⇒ | 搬送物の質量 | (Kg) |
|---|---|---|---|
| a | ⇒ | 搬送させる際の加速度 | (m/sec²) |
| g | ⇒ | 重力加速度(9.8) | (m/sec²) |
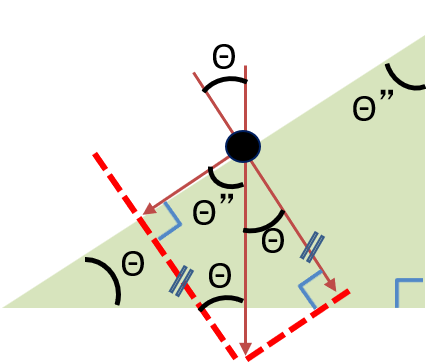
⑥補足(読みとばしOK)
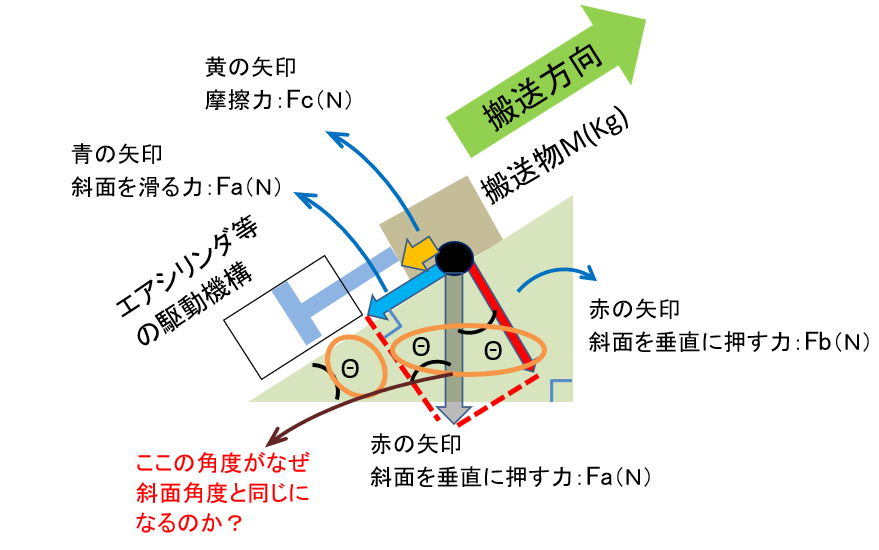
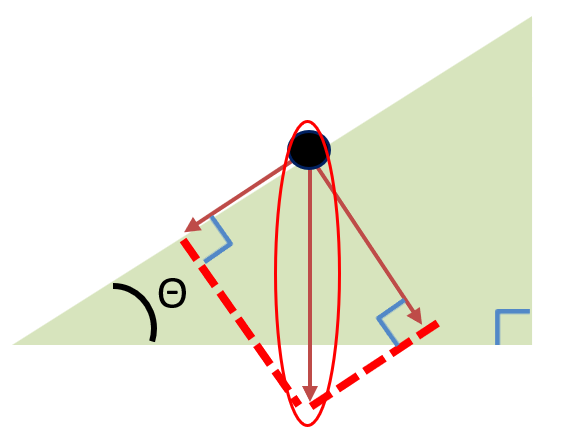
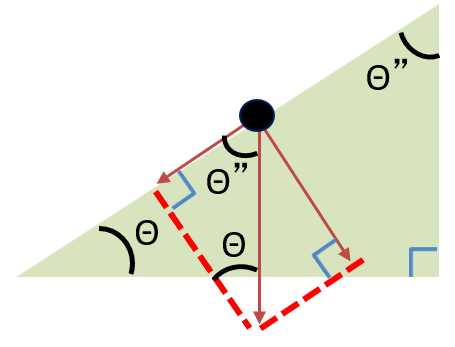
上図において なぜ力の分解ベクトルの角度が
斜面角度と同じになるのかを解説します。
|
まず、 すると・・・ |
|
|
右図より なので・・・ |
|
|
右図より なので・・・ |
|
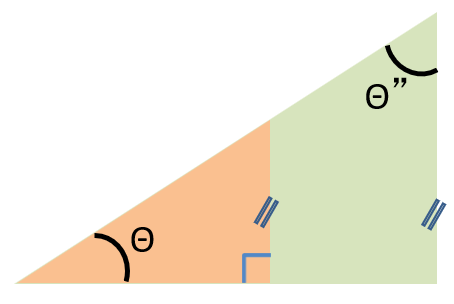
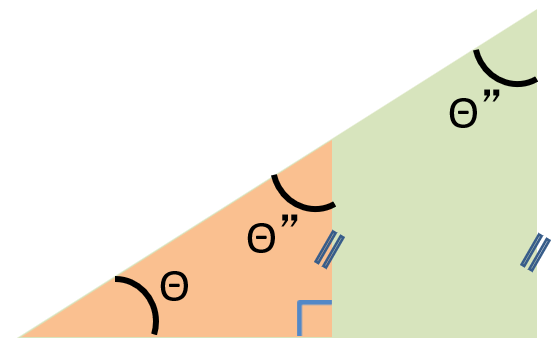
| 直角三角形の 内角より Θが証明されます。 |
|
| あとは平行線の 同位角と対頂角 により 右図が証明されます。 |
|
物体が単に斜面を
滑り落ちる場合
物体が単に斜面を滑り落ちる場合とは
以下の状況を指します。
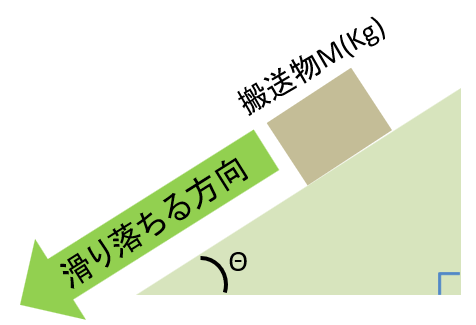
この時に注意したいのが摩擦力の向きです。
先ほどは、駆動系の搬送方向に対して
逆向きの摩擦力が発生しました。
しかし、摩擦力とは あくまで
進行方向の逆に発生する阻害する力
です。
今回のように滑る落ちる時に発生する
摩擦力は以下となります。
従って、
搬送物が斜面を自重で滑り落ちる力Ff(N)は
以下となります。
Ff=Mg・sin(Θ) - μMg・cos(Θ)
| Θ | ⇒ | 斜面の角度 | (°)もしくは (radian) |
|---|---|---|---|
| M | ⇒ | 搬送物の質量 | (Kg) |
| g | ⇒ | 重力加速度(9.8) | (m/sec²) |
| μ | ⇒ | 摩擦係数 | (無次元) |
⑦まとめ
汎用性のある式は、駆動機構が必要とする出力Fk(N)
Fk=Ma+Mg・sin(Θ)+μMg・cos(Θ)
この式は、水平時、垂直時 含めて、
全ての状態に対応しています。
本記事は以上です。
本記事を最後までお読み頂きありがとうございます。