本ブログの御訪問ありがとうございます
機械設計歴20年以上のtsurfと言います
今回は以下に関する記事です
【実際の計算例】ボールネジ機構における
サーボモーターの選定計算
⇩本記事は以下の方にオススメです⇩

未経験機械設計者
ボールネジを使った
サーボモーターの実際の計算例を
みたい
⇩本記事を読むと以下が わかります⇩

今回は基礎編の知識を前提に
ボールネジ機構の
サーボモーターを選定してみましょう
①条件
前置き
今回の記事は、サーボモーターの選定計算実践編です。
サーボモーターの選定計算の基礎については、
⇩以下の記事⇩を御参照ください。
この記事の解説に沿って計算をしていきます。
今回の駆動機構モデルは以下とします。
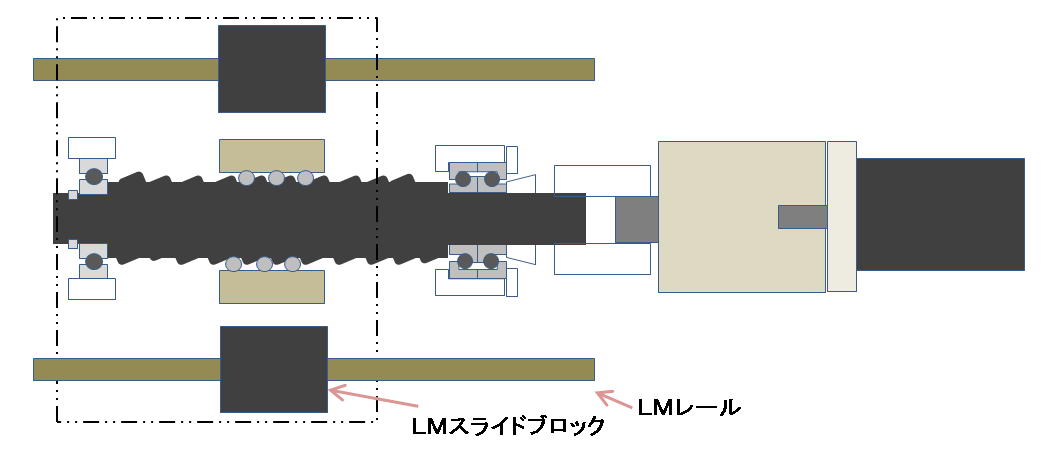
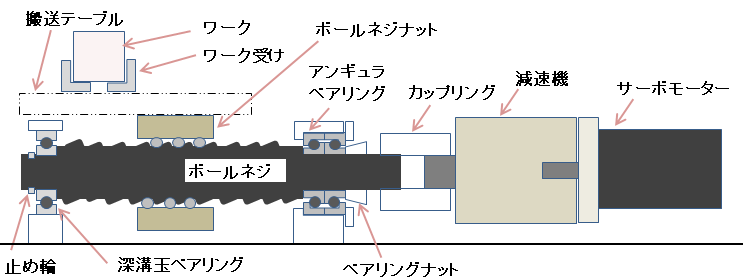
初期において想定可能な直動部品
直動部品において初期想定可能部品は以下となります。
この時点では ボールネジやLMガイドなどの仮選定も
できていないからです。
- ワーク重量 3(kg)
- ワーク受け重量 2(kg)
- 搬送テーブル 10(kg)
初期想定可能な直動部品総重量 15(kg)
位置決め条件
搬送姿勢は水平です
上記の機構でワークを複数の位置決め点数を移動しますが
一番条件が厳しい位置決め条件を以下とします。
- ストローク:50(mm)
- 移動時間:1(sec)
この条件がクリアできれば、後の位置決め条件は
クリアできるものとします。
補足
今回の例では、50wサーボモーター単体でも
問題ないのですが、減速機付きのもので解説をしたいため、
無理やり減速機をつけます。
②運転モデルの作成
運転モデルの検討
50(mm)を 1(sec)ということで、
以下のような運転パターンを、検討します。
- 加速時間と減速時間0.2(sec)
- 等速直線運動時間は0.6(sec)
グラフにすると、以下になります。
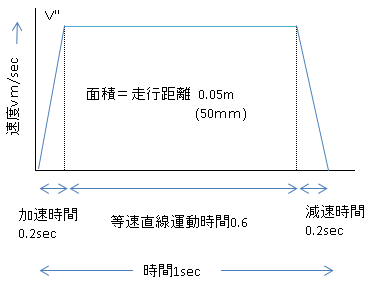
運転パターンの目的は 等速直線運動速度V”を求めて、
最終的に、加速トルクの算出に必要な角加速度を
求めるためです。
等速直線速度V”を求める
グラフを、以下に変換します。
四角形になり 簡単にV”を求めることができます。
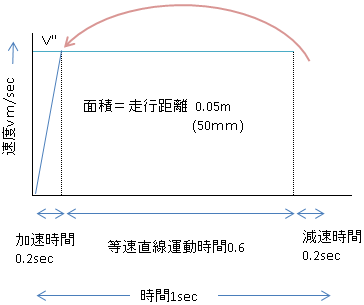
上記グラフより
等速直線運動速度V"
0.6(sec) × V”(m/sec)=0.05(m)より
V"=0.0625(m/sec)
③角速度と角加速度の算出
注意点
角速度はモーターの回転速度を毎秒あたりの回転角度を
弧度法にて表したものです。
ボールネジ機構なので、回転速度はボールネジにより
リードピッチに比例した直動速度に変換されます。
- 今回の場合 上記運転パターンで求めた
直動速度v”に到達できるための、回転速度を
求めなくてはいけません。 - サーボモーターの定格角速度が314(1/sec)なので
回転速度は、それ以下でなくてはいけません。
サーボモーターの定格角速度について
サーボモーターの定格回転数は3000rpmですが
角速度は毎秒あたりの弧度法表記ですので314(1/sec)となります。
換算法は1(回転) が 弧度法で2π(無次元)なので、
3000(rpm) ÷ 60(sec) × 2π=314(1/sec)となります。
リードピッチと減速比の仮検討と
角速度算出
ボールネジの仕様を以下としました。
- 外径:Φ20(mm)程度
- リードピッチ:5(mm)
外径Φ20mm前後のボールネジの中で
一番トルクが小さくてすむリードピッチを選択
減速比を1:3と仮設定しました
- この減速比はとりあえずの仮設定とします
最終的な結論次第では変更する可能性が高いです。
上記リードピッチ及び減速比と
直動速度V"=0.0625(m/sec)から角速度を求めます。
必要角速度ω”
=直動速度V”0.0625(m/sec) ÷ リードピッチPh 0.005(m) × 2π
× 減速比3(無次元)
=235.5(1/sec)
モーターの定格角速度314(1/sec)以内に収まりました
角加速度の算出
この時点で角加速度も求めましょう
角加速度ω”
=必要角速度ω 235.5(1/sec) ÷ 加速時間0.2(sec)
=1177.5(1/sec²)
仮決定要素
ここで 以下が仮決定しました
- ボールネジのリードピッチPh👉5(mm)
- 減速比👉1:3
- 必要角速度👉235.5(1/sec)
- 角加速度👉1177.5(1/sec²)
④外部摩擦トルクを算出
今回直動する部品は以下となります。

上記でボールネジのリードピッチを仮決定しましたので、
ボールネジの詳細な仮選定をしました。
ボールネジの詳細な仮選定
- リードピッチ:5mm
- 軸径:Φ20mm
- 全長500mm
ストロークとしては300mmできるもの
(他の位置でも位置決めするため)
ボールネジ仮選定の結果
ボールネジナットの重量は0.4Kg
LMガイドも適切なものを選定した結果
LMスライドブロックの重量0.4Kg × 2(ヶ)=0.8Kg
ここで初期想定可能直動部品の重量と合計すると以下となります。
直動部品総重量m(Kg)
=初期想定可能部品重量15(Kg)+ボールネジナットの重量0.4(Kg)
+LMスライドブロックの重量0.8(Kg)
= 16.2(Kg)
水平搬送なので外部摩擦力は以下となります。
外部摩擦力Fm(N)
=直動部品総重量16.2(Kg) × 重力加速度9.8(m/sec²)
× 摩擦係数0.1(無次元)*1
=15.9(N)
外部摩擦力とボールネジのリードピッチから
外部摩擦トルクの計算ができ、式は以下となります。
| = | 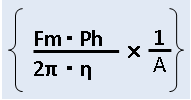 |
| 外部摩擦力 | 15.9 | ||
|---|---|---|---|
| リードピッチ | 0.005 | ||
| ボールネジ効率 | 0.95 | ||
| ボールネジの 減速比 |
3 |
よって外部負荷トルク=4.44E-3(Nm)
⑤加速トルクを求める(概要解説)
加速トルクは以下で求めることができます。
加速トルク = 慣性モーメント × 角加速度
角加速度はすでに 求めましたので、
慣性モーメントを算出することになります。
先述の参考記事を御参照願います。
簡単に説明すると、以下をそれぞれ算出します。
- 減速機の影響を受ける回転部品
- 減速機の影響を受けない回転部品
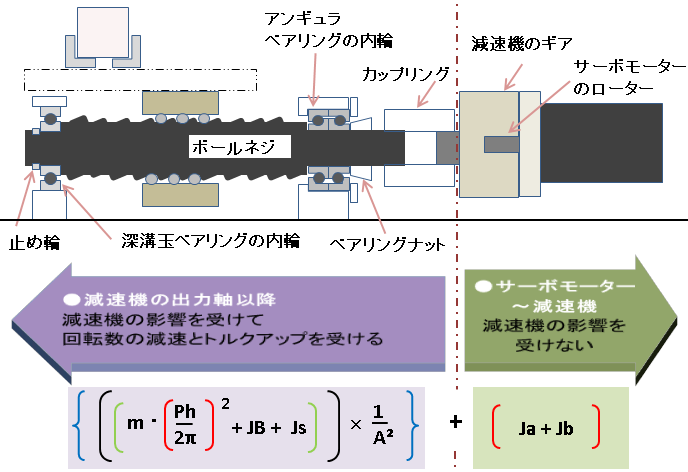
理由は、そのうち減速機の影響を受ける慣性モーメントは
減速比の影響の補正をしなくてはならないからです。
⑥加速トルクの算出
減速機の影響を受ける
慣性モーメントの範囲
以下の部品となります。
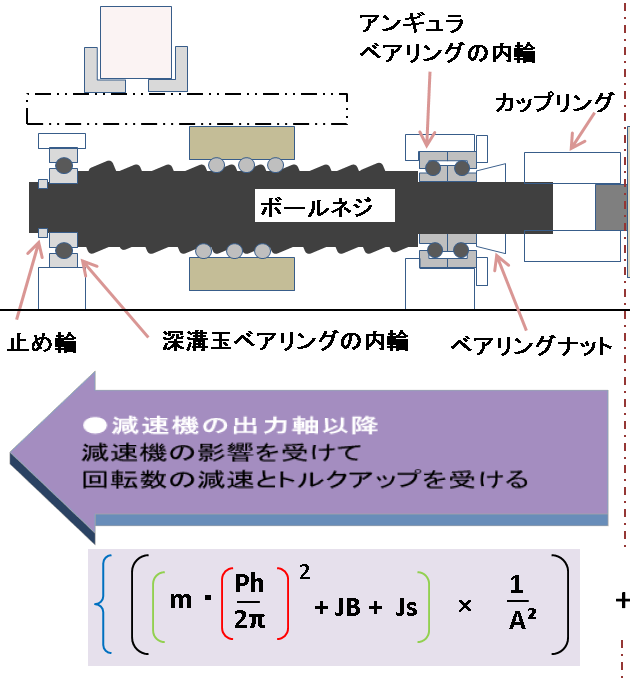
直動慣性モーメントの算出
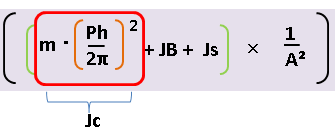
上記Jcとした部分は直動慣性モーメントとなります。
直動慣性モーメントとはボールネジが、
直動運動をさせられる際に発生する回転させづらさであり、
当然リードピッチに依存します。
m(Kg) 直動部品質量合計
Ph(m) リードピッチ
以上より
ボールネジが受ける直動慣性モーメントJc(Kg・m²)
=直動部品質量合計m 16.2(Kg)
× (リードピッチPh 0.005(m) ÷ 2π)²
=1.03E-5(Kg・m²)
ボールネジのそのものの
慣性モーメントJBの算出
JBはボールネジそのものの慣性モーメントとなります。
慣性モーメントに関しては近似計算をします。
慣性モーメントの式については
以下の記事を御参照願います。
まず 質量をもとめましょう。
ボールネジの材質は鉄系で、密度は8E-6(Kg/mm3)です
従って先述の仮選定より*2
ボールネジ質量mB(Kg):1.26(Kg)となります。
中心軸を回転する円柱の式を使い近似計算します。
ボールネジそのものの慣性モーメントJB(Kg・m²)
=(1/8) × ボールネジ質量 1.26(Kg) ×( 直径 0.02(m))²
=6.3E-5(Kg・m²)
その他の回転部品の
慣性モーメントJs
以下の慣性モーメントなどは小さい値なので無視します。
- ベアリングの内輪
- 止め輪
- ベアリングナット
しかし カップリングの慣性モーメントは結構大きいので
計算にいれましょう。
使用予定のカップリングの慣性モーメントが
カタログに記載がありました。
カップリングの慣性モーメント:1.7E-4(Kg・m²)
減速機の影響を受ける
慣性モーメント合計算出
以下の式より
慣性モーメント |
= |  |
減速機の影響を受ける慣性モーメント合計(Kg・m²)
={Jc 1.03E-5(Kg・m²) + JB 6.3E-5(Kg・m²) + Js 1.7E-4(Kg・m²)} × (1/3²)
=2.7E-5(Kg・m²)
サーボモーターから
減速機までの慣性モーメント算出
下の範囲は減速機の影響を受けない範囲となります。
- サーボモーターの回転軸
- 減速機

この2つは、だいたいカタログに記載があります。
サーボモーターの回転軸の慣性モーメント
は仮選定で50Wのもので検証します。
| 50Wのサーボモーター 回転軸慣性モーメント |
Ja | : | 4E-6 | (Kg・m²) |
|
減速機の慣性モーメント |
Jb | : | 9E-6 | (Kg・m²) |
慣性モーメント合計と加速トルク
全ての慣性モーメントの合計 × 角加速度となります。
加速トルク(Nm)
=(Jg 2.7E-5 + Ja 4E-6 + Jb 9E-6) × 角加速度ω”1177.5
=4.7E-2(Nm)
⑦必要トルクの算出と検証
必要トルク
=外部負荷トルク4.44E-5(Nm) + 加速トルク4.7E-2(Nm)
=5.15E-2(Nm)
よって必要トルク=5.15E-2(Nm)
ここで
K社の50Wサーボモーターを仮選定していますので、
比較していきます。
| K社 50W サーボモーター スペック |
計算結果 | ||
| トルク (Nm) |
0.16 |
> | |
|---|---|---|---|
| 角速度 (1/SEC) |
314 |
> | |
| 角加速度 (1/SEC²) |
40200 |
> | |
| 慣性モーメント (Kg・m²) |
1.4E-4 |
> |
補足 許容慣性モーメントについて*3
よって
今回の使用のサーボモーターは、仮選定での50Wのサーボモーターを使用
本記事は以上です
最後までお読みいただきありがとうございます。
*1:垂直搬送であれば摩擦係数はいりません
*2:
ボールネジの詳細な仮選定
- リードピッチ:5mm
- 軸径:Φ20mm
- ストロークとしては300mm
(他の位置でも位置決めするため) - 全長500mm
*3:
許容慣性モーメントは、そのサーボモーターで停止した時に
すぐに止まれるかどうか値です。
サーボモーターの回転軸の○○倍以下という表記になります。
今回 仮選定の
50Wのサーボモーターの回転軸の慣性モーメントは
4E-6(Kg・m²)です。
カタログに記載の許容慣性モーメントは
回転軸慣性モーメントの35倍以下なので、
許容慣性モーメント(Kg・m²)=4E-6(Kg・m²) × 35
=1.4E-4(Kg・m²)となります。
低速搬送で 減速時間も多く取れるのであれば、必ずしも
この数値に拘る必要がありませんが、
今回のようにすぐに止める必要がある場合、考慮が必要です。
もし、必要トルクがOKでも この値がオーバーするようであれば
ワンランク上のモーターにするなどの対応が必要となります。