本ブログの御訪問ありがとうございます。
機械設計歴20年以上のtsurfと言います。
今回は以下に関する記事です。
サーボモーターの選定計算
(トルク計算)の基礎 ボールネジ機構編
⇩本記事は以下の方にオススメです⇩

未経験機械設計者
ボールネジを使った
サーボモーターの選定計算について
知りたいんだけど
●計算式の意味が知りたい
●計算式の意味がわからないと実践できない
⇩本記事を読むと以下が わかります⇩

計算式をバラシて
わかりやすく説明します
- ①基本的知識 駆動力について
- ②解説用ボールネジ機構の解説と全体式の前説
- ③外部負荷トルクの計算式の仕組み と 計算式解説
- ④加速トルクの計算式の仕組み
- ⑤加速トルクの計算式の解説その1 減速機以降の慣性モーメント
- ⑥加速トルクの計算式の解説その2 サーボモーターから減速機の慣性モーメント
- ⑦加速トルクの計算式の解説その3 慣性モーメントの合算に角加速度をかける
- ⑧必要トルクの計算と モーター性能表との照らし合わせ
- ⑨実際の計算例
- ⑩歯車やプーリーを使った減速機構の場合
- ⑪まとめ
①基本的知識 駆動力について
基礎
サーボモーターの選定計算に関わらず、
ワークを搬送させるなどの駆動系の選定に共通して
必要な式は以下となります。
必要駆動力(N)=外部負荷力(N)+加速力(N)

このあたりを、
詳しく知りたい方は後回しても構わないので
以下の記事の御参照をお願いします
ただしモーターに関しては、トルクに変換した
以下となります。
必要駆動トルク(N・m)=外部負荷トルク(N・m)+加速トルク(N・m)
外部負荷トルク概要
(詳細は後述)
外部負荷力から外部負荷トルクを求めます。
外部負荷力とは実際に直動する部品の質量と
重力加速度から生じる、以下の力のことを指します。
- 垂直搬送であれば重力
- 水平搬送であれば摩擦力
この外部負荷力を
ボールネジのリードピッチからモーターのトルクに
変換したものが
外部負荷トルクです。
外部負荷トルクは直動機構を動かすにあたり
最低限必要な力であ、これだけでは動きません。
これから動き出すには、
加速力が必要になります。
加速トルク概要
(詳細は後述)
物体を動かし始める時には加速させる力
すなわち、加速力が必要です。
その加速力をモーターのトルクに変換したものです。
加速トルクは
慣性モーメントと角加速度の積です。
②解説用ボールネジ機構の解説と全体式の前説
解説用ボールネジ
機構のモデル
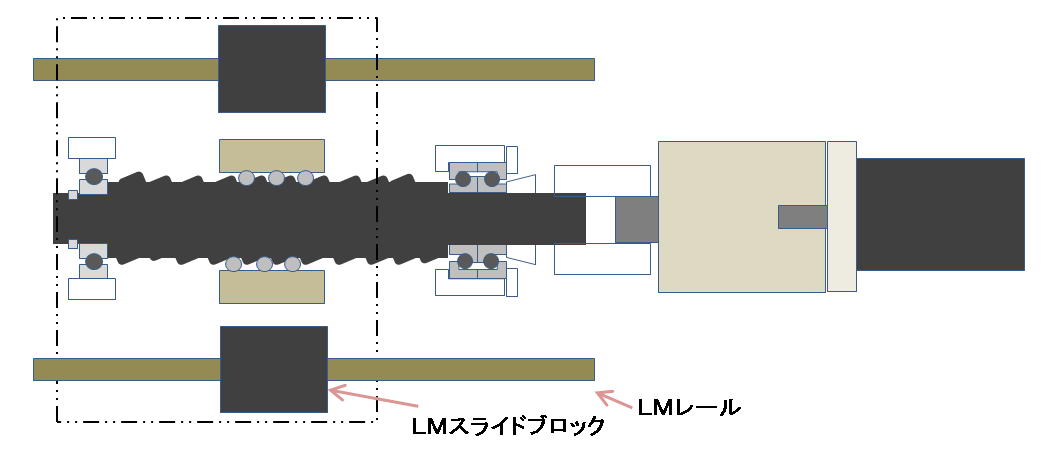
以下のようなモデルで、モーターの選定式を解説します。
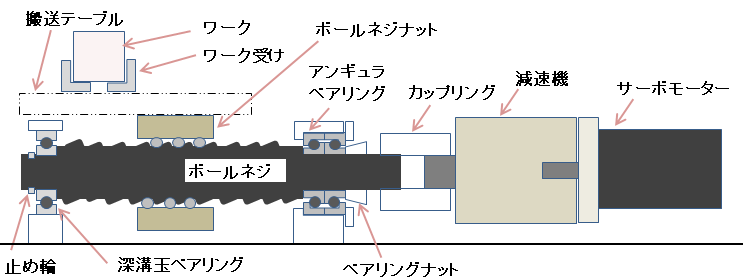
計算式前説
ボールネジ機構における
サーボモーターの選定で以下のような式を見かけます
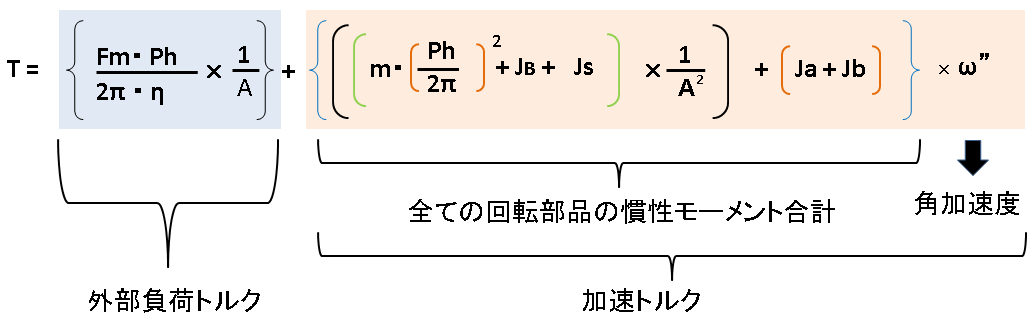
| 内容 | 単位 | 特記事項 | |
|---|---|---|---|
| T | モーターの必要トルク | N.m | |
| Fm | 直動部による外部負荷力 | N | 水平なら摩擦力 垂直なら重力 |
| Ph | ボールネジのリードピッチ | m | 単位換算に注意 |
| η | ボールネジ効率 | 無次元 | 0.9~0.95 |
| A | 減速比 | 無次元 | |
| m | 直動部の質量 | Kg | |
| JB | ボールネジの 慣性モーメント |
Kg.m² | |
| Js | その他回転部品の 慣性モーメント |
Kg.m² |
アンギュラベアリングの内輪 深溝玉ベアリングの内輪 ベアリングナット カップリングなど |
| Ja | 減速機の 慣性モーメント |
Kg.m² | カタログに記載あり |
| Jb | モーター軸の 慣性モーメント |
Kg.m² | カタログに記載あり |
| ω" | 角加速度 | 1/sec² |
※減速機をつけない場合は、以下で計算をします
- 減速比A=1
- 減速機の慣性モーメントJa=0
上記の計算式について、
①基本的知識で述べたことを踏まえつつ解説していきます。
⇩この部分が外部負荷トルクの計算部になります。
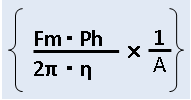
⇩この部分が 加速トルクの計算部になります 。
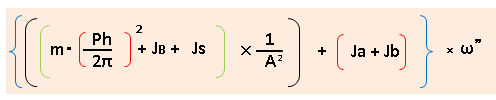
③外部負荷トルクの計算式の仕組み と 計算式解説
概要
以下の部分の計算式の解説をします。
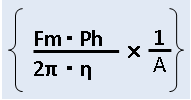
ここの部分は外部負荷力から
外部負荷トルクを計算しています。
図1の例では、直動する部分は以下となります。
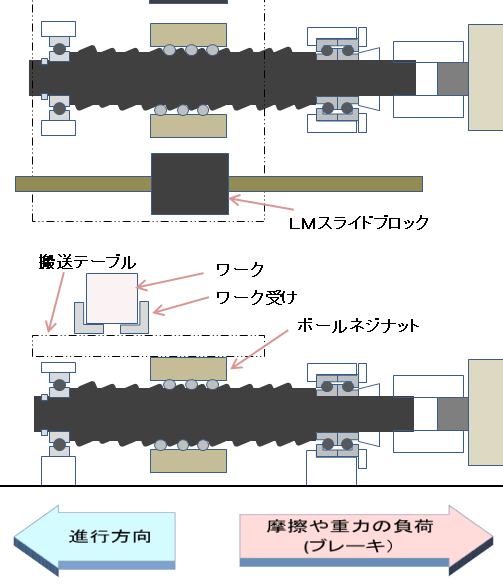
これらの部品は全て直動します。
そしてこれらの部品の質量は
以下のように直動方向に対して負荷(ブレーキ)となります。
- 垂直搬送であれば、重力として負荷
- 水平搬送であれ、LMレールに掛かり摩擦力
手順1 外部負荷力を求める
外部負荷力の式は、以下となります。
- 垂直搬送の外部負荷力(重力)
=直動部品の総質量×重力 - 水平搬送の外部負荷力(摩擦力)
=直動部品の総質量×重力×摩擦係数
では まず直動部品の総質量から求めましょう。
上図で直動する部品は、以下ですね。
- ワーク
- ワーク受け
- 搬送テーブル
- ボールネジナット(カタログに記載あり)
- LMスライドブロック(カタログに記載あり)
直動する部品の質量の合計である直動部品の総質量をmとします。
- 垂直搬送による重力をFmv
- 水平搬送による摩擦力をFmh
とすると各外部負荷力は以下の式になります。
垂直搬送による重力 Fm v = mg
水平搬送による摩擦力 Fm h = µmg
m:直動部質量合計 <Kg>
g:重力加速度 9.8 <m/sec²>
µ:摩擦係数 0.1<無次元>
補足 摩擦係数µ
ガイドを使う場合
カタログではガイドとレールの摩擦係数は0.05等ですが
安全を見て0.1で計算します
算出された計算結果を
⇩以下の赤枠の部分にあてはめます
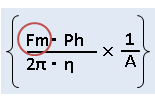
手順2 回転要素への変換式を掛ける
外部負荷力を外部負荷トルクに変換します。
ボールネジのリードピッチを2πで割ったものになります。
この式を掛けるとトルクへと換算されます。
⇩以下の部分です
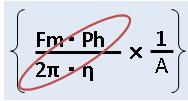
| Ph | ボールネジのリードピッチ | 単位(m) |
なお なぜPh÷2πをかけるとトルクへと変換されるかは
以下の記事を御参照ください。
手順3 ボールネジの効率を考慮する
ボールネジの効率ηを組み込みます。
係数なので無次元です
だいたい0.9~0.95で計算します。
⇩以下の部分です
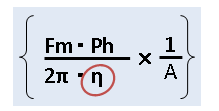
手順4 減速比を考慮する
減速機がつけば、減速される分トルクが大きくなります。
今求めているのはモーター軸にかかるトルクなので
減速比(無次元)で割ってあげています。
⇩以下の部分ですね
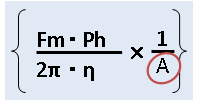
④加速トルクの計算式の仕組み
前置き
この章では、慣性モーメントと角加速度より加速トルクを求めます
慣性モーメントとは、物体の回転しづらさなのですが
詳しくは 以下の記事を御参照ください
概要
以下の計算式は加速トルクを計算しているのですが
その加速トルク算出を解説します。
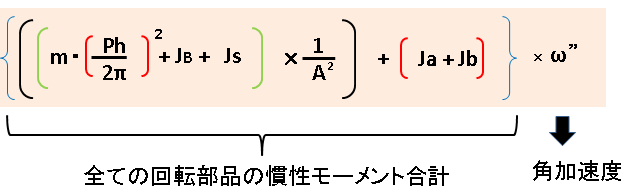
加速トルクは以下で求められます。
加速トルク(N)
=回転部品慣性モーメント(Kg・m²) × 角加速度(1/sec²)
図1の例では 回転する部品は以下となります。
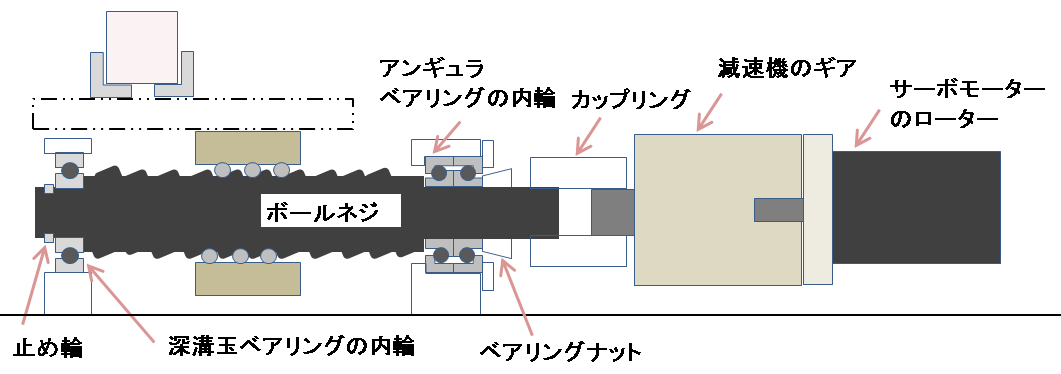
慣性モーメントは全回転部分に関して算出し、
合計するのですが
減速機のトルクアップによる影響があるかどうか
で以下に別れます
理由ですが
求めた慣性モーメントに、
減速機によるトルクアップの影響がある場合
回転しやすくなるので、計算値に補正をかけるからです。
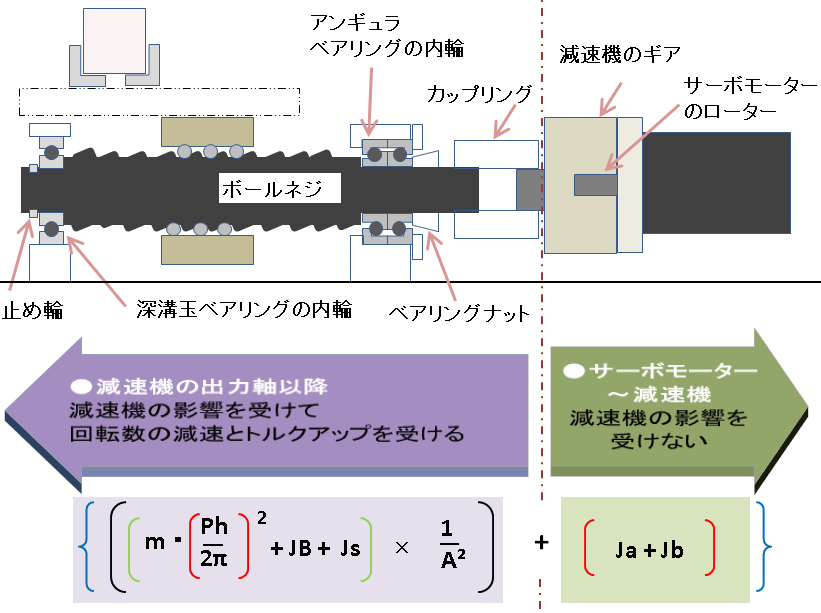
次章から 加速トルクの計算を解説します。
⑤加速トルクの計算式の解説その1
減速機以降の慣性モーメント
前解説 回転部品洗い出し(減速機以降)
以下の範囲の回転部品の慣性モーメントを算出します。
減速機以降で ひとまず括っている理由は、減速機以降の
回転部品は、減速機のトルクアップの影響を受けるので
補正が必要だからです。
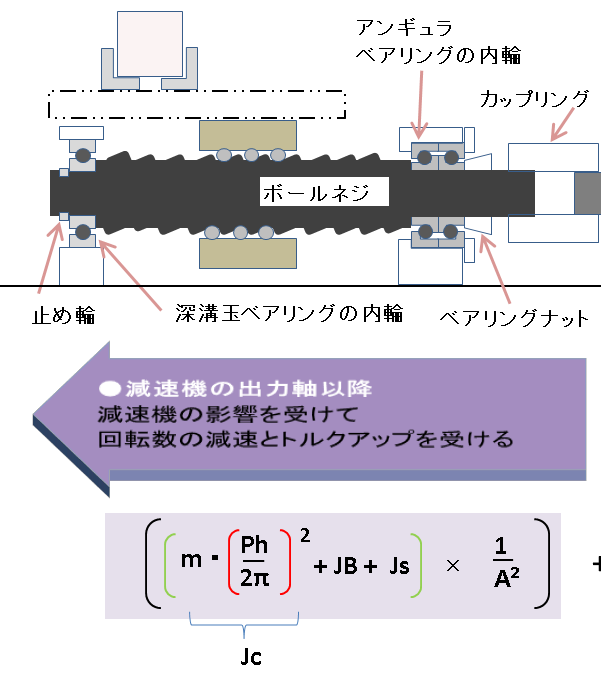
慣性モーメントは回転しづらさです。
この部分の慣性モーメントは、以下となります。
(詳しくは後述します)
| Jc | ➡ | ボールねじが直動部を直動させる際に発生する回転しづらさ |
| JB | ➡ | ボールネジ自体の回転させづらさ |
| Js | ➡ |
深溝玉ベアリングの内輪の回転させづらさ(小さいので無視) |
| アンギュラベアリングの内輪の回転させづらさ(小さいので無視) | ||
| 止め輪(小さいので無視) | ||
| ベアリングナットの回転させづらさ(小さいので無視) | ||
| カップリングの回転させづらさ |
手順1 直動慣性モーメントJc の算出
直動慣性モーメントとは・・・・
ボールネジが回転する際に直動部品を直動させるために発生する
回転させつらさ(=慣性モーメント)です
ボールネジの回転させづらさ(=慣性モーメント)
には以下があります。
- ボールネジ単体の回転させづらさ(JB)
- 直動部を直動させる際に発生する回転させづらさ(Jc)
しかし、この直動慣性モーメントJcは
ボールネジ単体の回転させづらさ(=慣性モーメント)
ではありません。
ボールネジが
直動部を直動送りする際に発生する負荷の
慣性モーメントとなります。
ボールネジによる直動慣性モーメントは、
以下の式で求めます。
=直動部の質量×(ボールネジのリードピッチ÷2π)²
⇩この赤枠の部分ですね
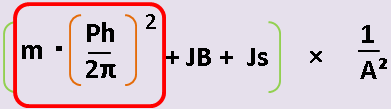
| Ph | ボールネジのリードピッチ | 単位(m) |
| m | 直動部の質量 (外部負荷力の算出時に求めた値です) |
単位(Kg) |
なぜ
直動部の質量×(ボールネジのリードピッチ÷2π)²で
直動慣性モーメントを求められるかは
以下の記事を御参照ください。
手順2 回転部品の慣性モーメントの算出
この手順2では、
単純な回転部品である以下の慣性モーメントを求めます。
- ボールネジそのものの慣性モーメント(JB)
- その他の回転部品の慣性モーメント(Js)
⇩この赤枠の部分です
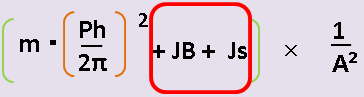
| JB | ボールネジそのものの慣性モーメント | 単位(Kg・m²) |
| Js |
以下の慣性モーメント合計
|
単位(Kg・m²) |
慣性モーメントの計算式については以下を御参照ください
注意点として
部品の形状を以下近似形状として計算してください
| ボールネジ | ➡ | 中実円柱の慣性モーメント計算式 |
| カップリング | ➡ | 中空円柱の慣性モーメント計算式 (カタログに記載がある場合が多い) |
手順3 減速比を考慮する
今まで計算してきた回転部は、減速機の影響を受けます。
減速比の2乗で割ってあげます。
⇩それが この赤枠の部分です
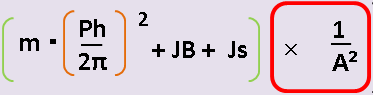
⑥加速トルクの計算式の解説その2
サーボモーターから減速機の慣性モーメント
これから計算する部分は、減速機の影響を受けません。
従って
この部分は、慣性モーメントを合算するだけです。
⇩この部分ですね
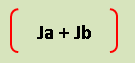
| Ja | ➡ | 減速機の慣性モーメント カタログに記載あり |
| Jb | ➡ | サーボモーターのローターの慣性モーメント カタログに記載あり |
⑦加速トルクの計算式の解説その3
慣性モーメントの合算に角加速度をかける
慣性モーメントの合算
今まで求めた
減速機以降の慣性モーメントと
サーボモーター~減速機までの慣性モーメントを合算します
⇩以下の赤枠の部分ですね

角加速度を掛けて
加速トルクの算出
慣性モーメントの合算に 角加速度を掛けます
⇩以下の赤枠の部分です
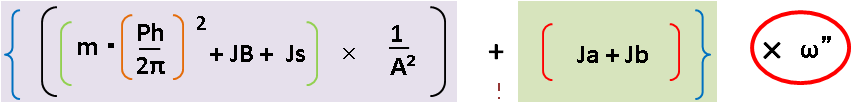
角加速度ω”について
角加速度は、
所定の回転数に到達するための回転加速度のことです。
簡単に解説すると以下になります。
ω”=ω / t a
ω:角速度 (1/sec)
ta: 加速時間 (sec)
しかし実際には、
運転時間と移動距離から
角加速度の求めることになりますので
以下の記事をご参照ください。
角速度はラジアン換算してください。
ラジアンは 角度によってできる円周の長さを半径で割った
比なので無次元です。
従って本ブログでは 角速度と角加速度の単位を以下としています。
- 角速度の単位は(rad/sec)ですが (1/sec)とする
- 角加速度の単位は(rad/sec²)ですが (1/sec²)とする
角速度や角加速度 及び弧度法の基礎知識については
以下を御参照ください。
⑧必要トルクの計算と モーター性能表との照らし合わせ
上記まで、外部負荷トルクと加速トルクが算出されましたので
冒頭の式にて外部負荷トルクと加速トルクを合計します。
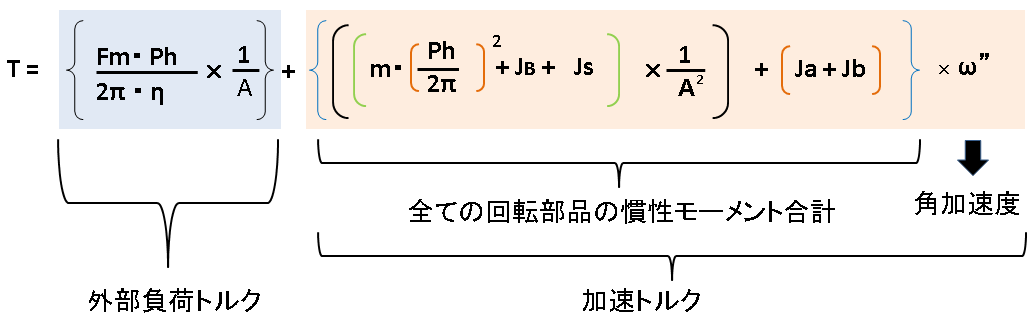
しかし、
選定計算を行っても モーター性能表の見方を間違えると
意味がありません。
以下の記事を御参照ください。
⑨実際の計算例
以下に 実際の計算例をまとめてあります。
ご参考ください
⑩歯車やプーリーを使った減速機構の場合
今回は減速機を使ったボールネジによる直動機構の
計算ですが
歯車やプーリーを使用した減速機構による選定計算については
以下をご参照お願いします。
⑪まとめ
- 基本は 以下となります
- 必要トルク=外部負荷トルク+加速トルク
- 外部負荷トルクは
外部の負荷である重力や摩擦力に対抗する最低限のものです - 動きださせるには 重力や摩擦力に加え 加速しなくてはいけません
- そのために 加速力が必要です
本記事は以上です。
最後までお読み頂きありがとうございます。