本ブログの御訪問ありがとうございます。
機械設計歴20年以上のtsurfと言います。
今回は以下に関する記事です
慣性モーメント(イナーシャ)とは
[わかりやすい慣性モーメントの考え方]
⇩本記事は以下の方にオススメです⇩

未経験機械設計者
モーターの選定計算を調べたら
慣性モーメントってでてきたけど何?
⇩本記事を読むと以下が わかります⇩

以下を 解説します
- 慣性モーメントとは物体の回りにくさ
- 慣性モーメントの考え方
- 最終的に何に使われるのか?
①結論(詳しくは後述)
慣性モーメントとは
慣性モーメントとは、以下となります。
物体の回転の回しにくさ
(=回転の止まりにくさ)
モーターやロータリーアクチュエーター等の回転駆動系の、
必要加速トルク計算を求める時に使います。
以下で、その物体を回転させる際の
加速トルクを求めることができます。
慣性モーメント × 角加速度=加速トルク
慣性モーメントを身近に感じる例
傘で例えてみましょう。
傘を閉じた状態で、回すと簡単に回りますよね。
しかし、傘を開いた状態で、回すと回転を重く感じます。
これは 空気抵抗ではりません。
傘を開いたことで、外径が大きくなり、慣性モーメントが
増大したのです。
結果 回転をさせるのに、大きな加速トルクが
必要になって回転が重くなったのです。
②物体が回転する際 角加速時に起こる事象
解説用モデル
| 右図のような の回転する円柱 を仮定します。 |
|
|
右図は、上記の |
|
そして下図は、
回転する円柱の上面図にあるA部の拡大図です。
以下 中心線上に、微小質点Ma と Mbを想定します
(注 微小質点とありますが 実際には線ですが・・・)
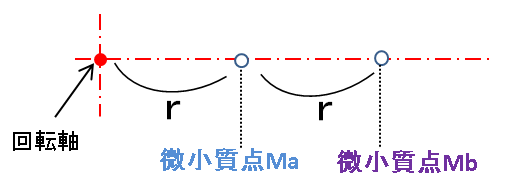
各微小質点の回転軸からの距離は以下となります。
微小質点Maの回転軸からの距離:r
微小質点Mbの回転軸からの距離:2 × r
微小質点Maと微小質点Mbの動きの説明
ここで 想定としては、この回転体が静止状態から
以下の条件で、角加速度運動を始めたとします。
| 角加速度 | ➡ | ω’ (1/sec2) |
| 加速時間 | ➡ | 微小時間⊿T秒 |
初期位置にいた 微小質点Maと微小質点Mbが、
角加速運動における微小時間(加速時間)⊿T秒後に、
⊿θ°回転して、以下の図の位置に移動しました。

ところで、微小質点Ma と 微小質点Mbの移動軌跡は、
微小時間ΔT秒間の移動なのでほぼ直線に近く
『微小時間⊿T秒の間は直線加速をしていた』
とみなせます
すると、上図を見てもあきらかなのですが、
微小質点Mbのほうが、微小質点Maに比べて移動距離が多いです。
つまり・・・・
⊿T秒間の直線加速度は、
微小質点Maより微小質点Mbのほうが、大きいということです。
③検証結果とその考察
考察1
検証から言えること
以上から言える事は、
これは微小時間ΔT秒間の角加速時間内の出来事なので
以下が言えます。
微小質点Maの直線加速度 < 微小質点Mbの直線加速度
微小質点Maと微小質点Mbの直線加速度は以下となります。
- aa=rω’
(aa:微小質点Maの直線加速度) - ab=2rω’
(ab:微小質点Mbの直線加速度)
考察2
考察1から言えること
考察1から言えることは、以下となります。
同じ回転体の中の微小質点でも、
外側の微小質点は、直線加速度が大きくなる
⇩ ⇩ ⇩
加速度が大きいということは、加速に必要な力も
大きくなります。
⇩ ⇩ ⇩
外側の微小質点であれば あるほど
必要な力が大きい=動かしにくいということです
つまり・・・
慣性モーメントは
この微小質点毎の動かしにくさ(=回転のしにくさ 止まりにくさ)
を図形の全面積分で、積分したものが慣性モーメントなのです。
ですから 冒頭で述べました傘を閉じた時と、傘を開いた時で
圧倒的に傘を開いた時に回しにくいのは これが理由なのです。
④慣性モーメントの式
⇩以下の記事を御参照ください⇩
⑤慣性モーメントの最終的な使い方
慣性モーメントは、回転体の回りにくさ(=止まりにくさ)です。
これに角加速度をかけると、必要加速トルクが算出できます。
⇩以下の記事を御参照ください⇩
最終的にモーターの必要トルク計算に繋げるのですが、
選定計算については、以下の記事を御参照ください。
⑥まとめ
- 慣性モーメントとは、物体の回しにくさ
- 慣性モーメントは、外径が大きいほど大きくなります。
- つまり 同じ重さでも、外径が大きくなるほど
物体は回しづらくなります。 - 慣性モーメントの式は 立方図形ごとに存在します。
- 最終的に角加速度を掛けて加速トルクを算出します。
- モーターやエアロータリーアクチュエーターの選定計算に
使われます
本記事は以上です。
最後まで お読みいただきありがとうございます。

