本ブログの御訪問ありがとうございます。
機械設計歴20年以上T.surfと言います。
今回は以下に関する記事です。
動的モーメントの基礎
単軸ロボット(ロボシリンダ)の選定
に必須知識
⇩本記事は以下の方にオススメです⇩

ロボシリンダ―
とかの動的モーメントの計算で
不明なところがあるよ
⇩本記事を読むと以下が わかります⇩

カタログだけでは
わかりづらい
動的モーメントの計算を
解説します。
①概要
動的モーメントの基礎的な考えですが
主にガイドなどの寿命に関係してきます。
静的モーメントに加速時の慣性力を考慮したものとなります。
慣性力については、以下の記事を御参照願います。
慣性力とは、加速方向の反対側に発生する
慣性が原因の見かけ上の力です。
加速時のみに慣性力が掛かるので
動的モーメントとは、
加速時のみガイドに対する負荷を言います。
②動的モーメントの基礎的な考え方
概要
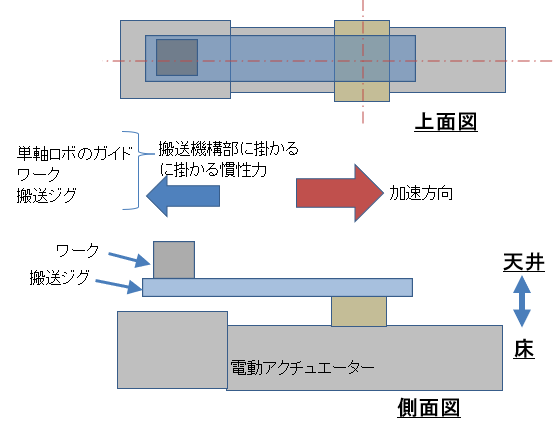
電動アクチュエーターのガイド部に
以下のような搬送ジグとワークによる搬送機構が
あり、加速方向と記載の方向に加速するとします。
単純に考えれば、加速時には以下のような
慣性力が掛かります。
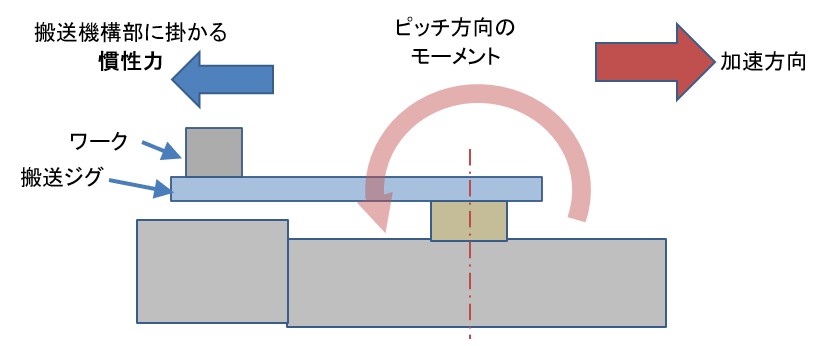
そして、以下の回転方向にガイドをひっぺ返そうとする
ピッチング方向に対するモーメントが掛かりますね。

慣性力によるモーメント
従って
慣性力のみを見た動的モーメントMKp(Nm)は、以下とすると
| 加速度 | a | (Nm) |
|---|---|---|
| ワークと 搬送ジグの 総重量 |
M | (Kg) |
| モーメント半径 | Lz | (Kg) |
以下の図より

MKp(Nm)=M(Kg)×a(m/sec²)×Lz(m)
となります。
重力によるモーメント
しかし、慣性力によるモーメントだけでは不十分です。
このモーメントは、回転によりガイドをひっぺ返そうとする
トルクなので、以下のような回転方向となりますよね?
なのでこの回転方向にもう一つのモーメントもありますよね?
これは静的モーメントですが、
以下の重力によるモーメントです。
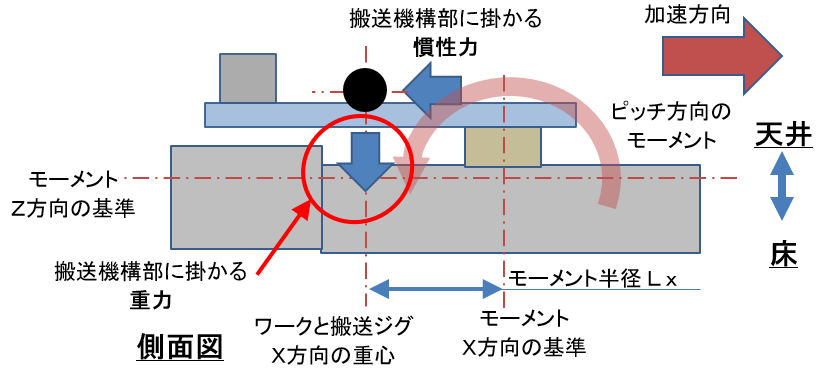
この重力のモーメントMGpは
| 重力加速度 | g | (Nm) |
|---|---|---|
| ワークと 搬送ジグの 総重量 |
M | (Kg) |
| モーメント半径 | Lx | (Kg) |
とすると、上図より
MGp(Nm)=M(Kg)×g(m/sec²)×Lx(m)
動的モーメントは・・
つまり、動的モーメントとは
加速時に掛かるモーメントの合計です。
従って、
- 慣性力によるモーメント
- 重量による静的モーメント
を合計しなくてはいけません。
動的モーメントMpは
Mp(Nm)
= M(Kg)×a(m/sec²)×LZ(m)
+M(Kg)×g(m/sec²)×Lx(m)
となります。
③重力によるモーメントがない動的モーメント
以下の場合は重力によるモーメントがありません。
水平で以下のように設置した場合の
ヨーイング方向の動的モーメントなどです。
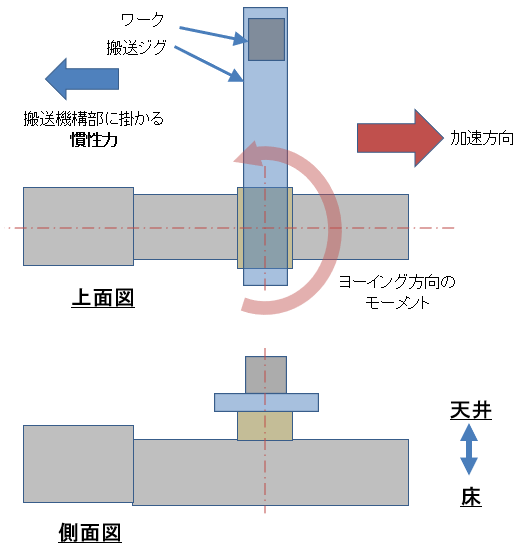
この場合は、
| 加速度 | a | (Nm) |
|---|---|---|
| ワークと 搬送ジグの 総重量 |
M | (Kg) |
| モーメント半径 | Lx | (Kg) |
とした場合、以下のようになるので

動的モーメントとしては
Myo(Nm)=M(Kg)×a(m/sec²)×Lx(m)
となります。
④その他の選定要素
基礎的な選定要素
ロボシリンダ―のわかりづらい
基本的な選定要素は以下の記事を御参照ください
- 可搬質量と加速度の関係
- 可搬質量と速度の関係
- ストロークと速度の関係
位置決め精度
位置決め精度については、2つの位置決め精度があります。
- 繰り返し位置決め精度
- ロストモーション
以下の記事を御参照願います。
⑤まとめ
- 動的モーメントは、加速時に掛かるモーメント
- ガイドなどの寿命に関わってくる
- 動的モーメントは慣性力によるモーメントと
重力によるモーメントの合計 - 慣性力とは、加速力の逆向きに働く見かけ上の力
- 動的モーメントは、重力によるモーメントがない場合もある。
本記事は以上です。
最後までお読みいただきありがとうございます。